問題
流体の基礎に関する次の文章の( )内に入る語句の組合せとして、正しいものはどれか。
摩擦のないダクト中を進む流れを考え、流れの上流側にA断面、下流側にB断面をとる。ダクト内の流管の二つの断面A、Bにおける流れの力学的エネルギーの保存を仮定すると次のようなベルヌーイの定理を表す式が得られる。
ただし、ρ:密度、a:( ア )、b:( イ )、g:重力加速度、c:( ウ )とする。
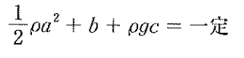
| ア | イ | ウ | |
| 1. | 速度 | 静圧 | 高さ |
| 2. | 速度 | 動圧 | 高さ |
| 3. | 高さ | 静圧 | 速度 |
| 4. | 静圧 | 高さ | 速度 |
| 5. | 動圧 | 高さ | 速度 |
回答と解説動画
正解は(1)
この問題の正しい組合せは
ア:速度 イ:静圧 ウ:高さ
です。
ベルヌーイの定理は、流体のエネルギー保存則を表す法則です。
この定理によると、流れの中のある2点(A点、B点)で、
「運動エネルギー(動圧)」「圧力エネルギー(静圧)」「位置エネルギー(位置圧)」の合計が一定になります。
$$ \frac{1}{2} \rho v^2 + P + \rho g h = \text{一定} $$
- ρ(ロー):流体の密度
- v:流速(速度)
- P:圧力(静圧)
- g:重力加速度
- h:高さ
各項の意味.
\(\frac{1}{2} \rho v^2\) → 動圧(流体の運動エネルギーを圧力で表したもの)
P → 静圧(流体が持つ圧力エネルギー)
\(\rho g h\) → 位置圧(高さによる位置エネルギー)
現実の流れで生じるもの
実際の流れでは、管内の摩擦や乱流などによって圧力損失(エネルギー損失)が発生します。
そのため、理想的なベルヌーイの式の左辺と右辺は完全には等しくなりません。
ポイント
- 動圧・静圧・位置圧の意味と式中の位置を正確に覚えること
- 圧力損失が現実の流れで必ず発生すること
- ベルヌーイの定理は、配管や空調ダクトの流体計算の基本公式
- ビル管理士の試験ではベルヌーイの定理を用いた計算問題は出題されないので、用語の意味さえわかっていればOK
解説動画
解説動画はまだありません

コメント